So, what do we do for
ZL? A quick glance at a transmission line problem shows that at
the load we have a resistor and an inductor in parallel. This
was done on purpose, to show you one of the powerful aspects of
the Smith Chart. Based on what you know from circuit theory you
would calculate the load impedance by using the formula for two
impedances in parallel
ZL=
which will be somewhat messy to calculate.
Let's remember the formula for what the Smith
Chart represents in terms of the phasor
r(s).
Let's invert this expression
Equation 3 says that is we want to get an
admittance instead of an impedance, all we have to
do is substitute
−(r(s)) for
r(s) on the Smith Chart plane!
in our case. We have two elements in parallel for
the load (
YL=Y+ⅈB), so we can easily add their admittances, normalize them to
Y0, put them on the Smith Chart, go
180° around (same thing as letting
−(r(s))=r(s)) and read off
. For a
200Ω resistor,
G, the
condunctance equals
=0.005.
Y0=0.02 so
=0.25. The generator is operating at a frequency of
<apply>200MHz</apply>, so
ω=2πf=1.25×109s-1 and the inductor has a value of
160nH, so
ⅈωL=200ⅈ and
B=
=-0.005ⅈ and
=-0.25ⅈ.
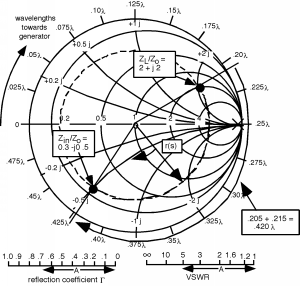
We plot this on the Smith
Chart by first finding the real part = 0.25 circle, and
then we go down onto the lower half of the chart since that is
where all the negative reactive parts are, and we find the curve
which represents
-0.25ⅈ and where they intersect, we put a dot, and mark the
location as
. Now to find
, we simply reflect half way around to the opposite
side of the chart, which happens to be about
=2+2ⅈ, and we mark that as well. Note that we can take the
length of the line from the center of the Smith Chart to our
and move it down to the
|Γ| scale and find that the reflection coefficient has a
magnitude of about 0.6. On a real Smith Chart, there is also a
phase angle scale on the outside of the circle (where our
distance scale is) which you can use to read off the phase angle
of the reflection coefficient as well. Putting that scale on
the "mini Smith Chart" would clog things up too much, but the
phase angle of
Γ is about
3.0°.
Now the wavelength of the signal on the line is
given as
The input to the line is located
21.5cm or
0.215λ away from the load. Thus, we start at
, and rotate around on a circle of constant radius a
distance
0.215λ towards the generator. To do this, we extend a line out from
our
point to the scale and read a relative distance of
0.208λ. We add
0.215λ to this, and get
0.423λ Thus, if we rotate around the Smith Chart, on our
circle of constant radius Since, after all, all we are doing is
following
r(s) as it rotates around from the load to the input to the line.
When we get to
0.423λ, we stop, draw a line out from the center, and where
it intercepts the circle, we read off
from the grid lines on the
Smith
Chart. We find that
Thus,
Zin=15−25ⅈ ohms
Figure 3. Or, the impedance at the
input to the line looks like a
15Ω resistor in series with a capacitor whose reactance
ⅈX=-25ⅈ, or, since
Xcap=
, we find that,
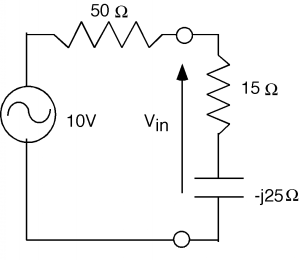
To find
Vin, there is no avoiding doing some complex math:
Which, we write in polar notation, divide, figure the voltage
and then return to rectangular notation.
| Vin |
= |
0.418∠-38×10 |
|
= |
4.18∠-38 |
|
= |
3.30−2.58ⅈ |
(9)
If at this point we needed to find the actual voltage phasor
V+ we would have to use the equation
| Vin |
= |
V+ⅇⅈβL+ΓV+ⅇ−(ⅈβL) |
|
= |
V+ⅇⅈβL+|Γ|V+ⅇⅈ(θr−βL) |
(10)
Where
β=
is the propagation constant for the line as mentioned
in the
last
chapter, and
L is the
length of the line.
For this example,
βL=
0.215λ=1.35radians and
θΓ=Γ=0.52radians. Thus we have:
Vin=V+ⅇⅈ1.35+0.52V+ⅇⅈ(0.52−1.35)
(11)
Which then gives us:
V+=
| Vin |
| ⅇⅈ1.35+0.52ⅇⅈ(0.52−1.35) |
(12)
When you expand the exponentials, add and combine in rectangular
coordinates, change to polar, and divide, you will get a phasor
value for
V+. If you do it correctly, you will find that
V+=5.04∠-71.59
Many times we don't care about
V+itself, but are more interested in how much power is being
delivered to the load. Note that power delivered to the input
of the line is also the amount of power which is delivered to
the load! Finding
Iinis easy, it's just
. All we have to do is change
Zin to polar form.

"This course offers an introduction to solid state device including field effect and bipolar transistors. Properties of transmission lines and propagating E&M waves are also presented. It is […]"